Piston Speed Stroke to RPM Calculator

Piston Speed (\( pS \)):

Stroke (\( s \)):

Engine RPM (\( \text{RPM} \)):

1. What is the RPM (Piston Speed, Stroke) Calculator?

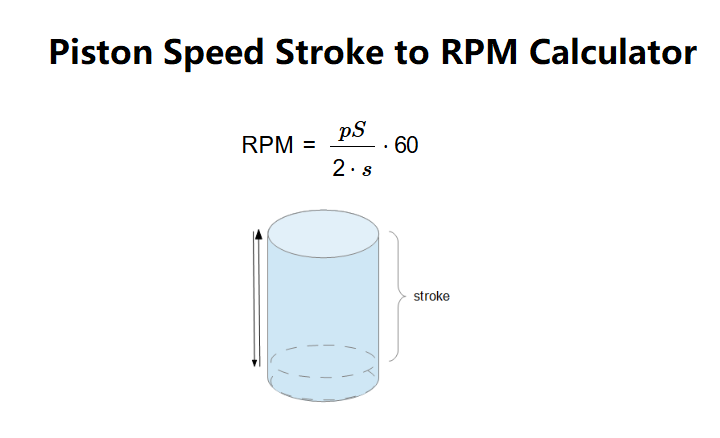
Definition: This calculator computes the engine RPM (\( \text{RPM} \)) based on the average piston speed (\( pS \)) and stroke length (\( s \)).

Purpose: It is used in automotive and mechanical engineering to determine the engine speed (in revolutions per minute) required to achieve a given piston speed, which is critical for engine design and performance analysis.

2. How Does the Calculator Work?

The calculator uses the following relationship:

\[ \text{RPM} = \frac{pS}{2 \cdot s} \cdot 60 \]

Where:

\( \text{RPM} \) — Engine speed in revolutions per minute
\( pS \) — Average piston speed (in various units)
\( s \) — Stroke length (distance the piston travels in one cycle)

Explanation: Enter the piston speed and stroke length in the chosen units, and the calculator computes the engine RPM. The piston speed is converted to inches per second, and the stroke is converted to inches for the calculation. The RPM is calculated by first determining the revolutions per second (\( \text{RPS} = \frac{pS}{2 \cdot s} \)) and then converting to RPM by multiplying by 60. The result is displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For default inputs (\( pS = 10 \, \text{m/s} \), \( s = 0.1 \, \text{m} \)), the calculated RPM is approximately 3000.00000, matching the example from the Piston Speed Calculator.

3. Importance of RPM (Piston Speed, Stroke) Calculation

Details: Calculating the RPM based on piston speed and stroke is essential for designing engines and ensuring they operate within safe limits. Piston speed affects engine durability and performance, and this calculation helps engineers determine the engine speed required to achieve a desired piston speed, optimizing for power, efficiency, and longevity.

FAQ

How do I find the engine RPM from piston speed and stroke?

Measure the piston speed (\( pS \)) in inches per second and the stroke (\( s \)) in inches. Compute the RPM using the formula \( \text{RPM} = \frac{pS}{2 \cdot s} \cdot 60 \). The result will be in revolutions per minute.

What does engine RPM represent?

Engine RPM (\( \text{RPM} \)) represents the number of revolutions per minute that the engine's crankshaft completes, indicating the engine's operating speed.

What is the formula for RPM based on piston speed and stroke?

The formula for RPM is \( \text{RPM} = \frac{pS}{2 \cdot s} \cdot 60 \), where \( pS \) is the piston speed, and \( s \) is the stroke length. The result is in revolutions per minute.

Can I use different units for piston speed and stroke?

Yes, the calculator supports multiple units for piston speed (metres/second, millimeter/second, centimeter/second, miles per hour, inch/second, inch/minute, foot/second, foot/minute) and stroke (inches, centimeters, millimeters, meters, feet). All inputs are converted to inches per second and inches, respectively, for the calculation.

What happens if I enter zero for piston speed or stroke?

Entering zero for piston speed (\( pS \)) or stroke (\( s \)) will result in the calculation not being performed, as these values must be greater than zero for a valid result.

Favorite