Multiple Pulley Calculator

Multiple Pulley Calculator - Pulley and Effort Force Calculator

Mass (\( m \)):

Mechanical Efficiency (\( \mu \)):

Number of Ropes (\( n \)):

Gravitational Constant (\( g \)):

Effort Force (\( S \)) in Newtons (N):

Effort Force (\( S \)) in Kilonewtons (kN):

Effort Force (\( S \)) in Pounds force (lbf):

1. What is the Blocks and Tackles Calculator?

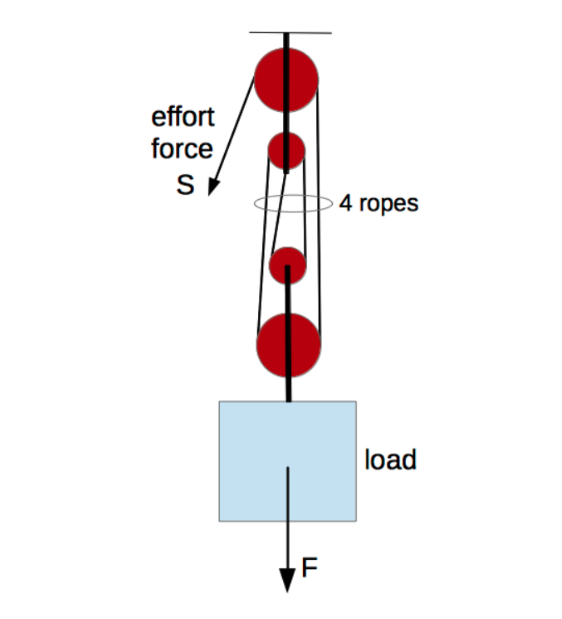
Definition: This calculator computes the effort force (\( S \)) required to raise or pull a load using a block and tackle system, based on the mass (\( m \)), gravitational constant (\( g \)), mechanical efficiency (\( \mu \)), and number of ropes (\( n \)).

Purpose: It is used in mechanical engineering and physics to determine the force needed to lift a load with a pulley system, accounting for mechanical advantage and efficiency losses.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ S = \frac{m \cdot g}{\mu \cdot n} \]

Where:

\( S \) — Effort force (in various units)
\( m \) — Mass (in kg, g, lb, oz, tons, US gallons, or UK gallons)
\( g \) — Gravitational constant (9.81 m/s² or 32.17405 ft/s²)
\( \mu \) — Mechanical efficiency of the system (0 to 1)
\( n \) — Number of ropes between the sets of pulleys

Explanation: Enter the mass, mechanical efficiency, number of ropes, and gravitational constant in the chosen units. The mass is converted to kilograms, and the gravitational constant is converted to m/s². The effort force is calculated as \( S = \frac{m \cdot g}{\mu \cdot n} \), where the result is the force in Newtons. Results are displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For default inputs (\( m = 100 \, \text{kg} \), \( \mu = 1 \), \( n = 1 \), \( g = 9.81 \, \text{m/s}^2 \)), the calculated effort force \( S \) is approximately 981.00000 N.

3. Importance of Blocks and Tackles Calculation

Details: Calculating the effort force for a block and tackle system is essential for designing lifting mechanisms, optimizing mechanical advantage, and accounting for efficiency losses in real-world applications such as cranes and hoists.

FAQ

How do I calculate the effort force for a block and tackle system?

Measure the mass (\( m \)), mechanical efficiency (\( \mu \)), number of ropes (\( n \)), and gravitational constant (\( g \)). Compute the effort force using the formula \( S = \frac{m \cdot g}{\mu \cdot n} \). The result will be in Newtons (N).

What does the effort force represent?

The effort force (\( S \)) represents the force required to lift a load, adjusted by the mass, gravitational constant, mechanical efficiency, and number of ropes in a block and tackle system.

What is the formula for the effort force in a block and tackle?

The formula for the effort force is \( S = \frac{m \cdot g}{\mu \cdot n} \), where \( m \) is the mass, \( g \) is the gravitational constant, \( \mu \) is the mechanical efficiency, and \( n \) is the number of ropes. The standard unit for force in this calculator is Newtons (N).

Can I use different units for mass and other parameters?

Yes, the calculator supports multiple units for mass (g, kg, lb, oz, tons, US gallons, UK gallons), gravitational constant (m/s², ft/s²), and efficiency (as a fraction). All inputs are converted to kilograms and m/s² for the calculation.

What happens if I enter zero for the number of ropes or efficiency?

Entering zero for the number of ropes (\( n \)) or efficiency (\( \mu \)) will result in the calculation not being performed, as the formula involves division by these values. Both must be greater than zero (efficiency ≤ 1) for a valid result.

Favorite