Calculadora de Longitud de Correa

Primer Diámetro (\( P_D \)):

Segundo Diámetro (\( S_D \)):

Distancia entre los Ejes (\( L \)):

Longitud de la Correa (\( BL \)) en metros (m):

Longitud de la Correa (\( BL \)) en pies (ft):

Longitud de la Correa (\( BL \)) en centímetros (cm):

Longitud de la Correa (\( BL \)) en pulgadas (in):

1. ¿Qué es la Calculadora de Longitud de Correa?

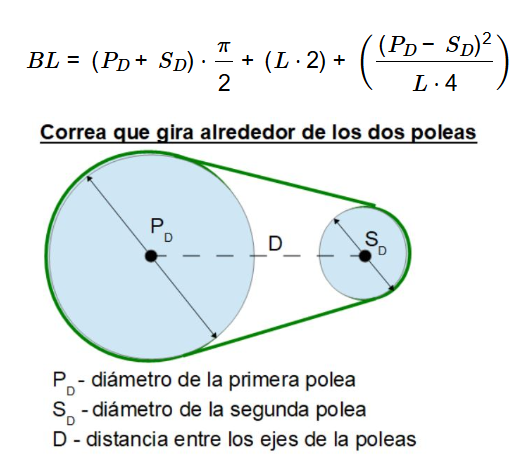
Definición: Esta calculadora determina la longitud de la correa (\( BL \)) necesaria para conectar dos poleas, basándose en los diámetros de las poleas (\( P_D \) y \( S_D \)) y la distancia entre sus ejes (\( L \)).

Propósito: Se utiliza en ingeniería mecánica para calcular la longitud correcta de la correa en sistemas de poleas, aplicable en maquinaria, sistemas automotrices y equipos industriales.

2. ¿Cómo Funciona la Calculadora?

La calculadora utiliza la relación:

\[ BL = (P_D + S_D) \cdot \frac{\pi}{2} + (L \cdot 2) + \left( \frac{(P_D - S_D)^2}{L \cdot 4} \right) \]

Donde:

\( BL \) — Longitud de la correa (en varias unidades)
\( P_D \) — Diámetro de la primera polea (Primer Diámetro)
\( S_D \) — Diámetro de la segunda polea (Segundo Diámetro)
\( L \) — Distancia entre los ejes (La extensión de la fuerza en un eje)

Explicación: Ingresa los diámetros de las dos poleas y la distancia entre sus ejes en las unidades elegidas, y la calculadora determinará la longitud de la correa. Todas las entradas se convierten a metros para el cálculo, y el resultado se convierte a varias unidades para su visualización. Los resultados se muestran con 5 decimales, usando notación científica si el valor excede 100,000 o es menor a 0.0001. Para las entradas predeterminadas (\( P_D = 1 \, \text{m} \), \( S_D = 0.5 \, \text{m} \), \( L = 2 \, \text{m} \)), la longitud de la correa calculada \( BL \) es aproximadamente 6.38744 metros.

3. Importancia del Cálculo de la Longitud de la Correa

Detalles: Calcular la longitud correcta de la correa es esencial para garantizar una transmisión de potencia eficiente en sistemas de poleas, prevenir deslizamientos y prolongar la vida útil de las correas en aplicaciones mecánicas.

Preguntas Frecuentes

¿Cómo calculo la longitud de la correa para un sistema de poleas?

Mide los diámetros de las dos poleas (\( P_D \) y \( S_D \)) y la distancia entre sus ejes (\( L \)) en metros. Calcula la longitud de la correa usando la fórmula \( BL = (P_D + S_D) \cdot \frac{\pi}{2} + (L \cdot 2) + \left( \frac{(P_D - S_D)^2}{L \cdot 4} \right) \). El resultado estará en metros.

¿Qué representa la longitud de la correa?

La longitud de la correa representa la longitud total necesaria para conectar dos poleas, considerando las circunferencias de las poleas y la distancia entre sus ejes.

¿Cuál es la fórmula para la longitud de la correa?

La fórmula para la longitud de la correa es \( BL = (P_D + S_D) \cdot \frac{\pi}{2} + (L \cdot 2) + \left( \frac{(P_D - S_D)^2}{L \cdot 4} \right) \), donde \( P_D \) y \( S_D \) son los diámetros de las poleas, y \( L \) es la distancia entre los ejes. La unidad estándar para la longitud de la correa en esta calculadora es metros.

¿Puedo usar diferentes unidades para los diámetros de las poleas y la distancia?

Sí, la calculadora admite múltiples unidades para los diámetros de las poleas y la distancia, incluyendo metros, pies, centímetros y pulgadas. Todas las entradas se convierten a metros para el cálculo.

¿Qué pasa si ingreso cero para la distancia entre los ejes?

Ingresar cero para la distancia entre los ejes (\( L \)) hará que el cálculo no se realice, ya que la fórmula implica una división por \( L \). La distancia debe ser mayor que cero para obtener un resultado válido.

Favorito